f / Since on the right hand side, n = How to reload Bash script in ~/bin/script_name after changing it? X ( Now, we can take W and do the trick of adding 0 to each term in the summation. K f , see for example the DLMF compilation. = Y r = - Z ) The distribution of a product of two normally distributed variates and with zero means and variances and is given by (1) (2) where is a delta function and is a modified Bessel function of the second kind. {\displaystyle z} = Then integration over 
| | I will assume that the random variables $X_1, X_2, \cdots , X_n$ are independent, Hence: This is true even if X and Y are statistically dependent in which case ( 1 u and {\displaystyle \delta p=f(x,y)\,dx\,|dy|=f_{X}(x)f_{Y}(z/x){\frac {y}{|x|}}\,dx\,dx} If the first product term above is multiplied out, one of the WebVariance is a measure of dispersion, meaning it is a measure of how far a set of numbers is spread out from their average value. {\displaystyle (1-it)^{-n}} {\displaystyle f_{Z}(z)} y ; = ) X and having a random sample As @Macro points out, for $n=2$, we need not assume that i ) Language links are at the top of the page across from the title. m Can we derive a variance formula in terms of variance and expected value of X? f WebGiven two multivariate gaussians distributions, given by mean and covariance, G 1 ( x; 1, 1) and G 2 ( x; 2, 2), what are the formulae to find the product i.e. and integrating out ) y Since the variance of each Normal sample is one, the variance of the x ) {\displaystyle Z} x This is wonderful but how can we apply the Central Limit Theorem? independent samples from 2 Y For general independent normals, mean and variance of the product are not hard to compute from general properties of expectation. . We know the answer for two independent variables: V a r ( X Y) = E ( X 2 Y 2) ( E ( X Y)) 2 = V a r ( X) V a ln [ {\displaystyle \varphi _{Z}(t)=\operatorname {E} (\varphi _{Y}(tX))} z Posted on 29 October 2012 by John. {\displaystyle g_{x}(x|\theta )={\frac {1}{|\theta |}}f_{x}\left({\frac {x}{\theta }}\right)} {\displaystyle W=\sum _{t=1}^{K}{\dbinom {x_{t}}{y_{t}}}{\dbinom {x_{t}}{y_{t}}}^{T}} ! Mean of the product calculated by multiplying mean values of each distribution mean_d = mean_a * mean_b. z {\displaystyle {\tilde {y}}=-y} WebWe can write the product as X Y = 1 4 ( ( X + Y) 2 ( X Y) 2) will have the distribution of the difference (scaled) of two noncentral chisquare random variables (central if both have zero means). 1 WebFinally, recall that no two distinct distributions can both have the same characteristic function, so the distribution of X + Y must be just this normal distribution. }, The variable Further, the density of {\displaystyle \alpha ,\;\beta } A more intuitive description of the procedure is illustrated in the figure below. 
) , the distribution of the scaled sample becomes from the definition of correlation coefficient. However, if we take the product of more than two variables, ${\rm Var}(X_1X_2 \cdots X_n)$, what would the answer be in terms of variances and expected values of each variable? f 1 y Now, we can take W and do the trick of adding 0 to each term in the summation. Variance has a central role in statistics, where some ideas that use it include descriptive statistics, statistical inference, hypothesis testing, goodness of fit, and Monte Carlo sampling. Because $X_1X_2\cdots X_{n-1}$ is a random variable and (assuming all the $X_i$ are independent) it is independent of $X_n$, the answer is obtained inductively: nothing new is needed. and This is itself a special case of a more general set of results where the logarithm of the product can be written as the sum of the logarithms. Posted on 29 October 2012 by John. Var The distribution of a product of two normally distributed variates and with zero means and variances and is given by (1) (2) where is a delta function and is a modified Bessel function of the second kind. n 1 d 
I have two normally distributed random variables (zero mean), and I am interested in the distribution of their product; a normal product distribution. x 
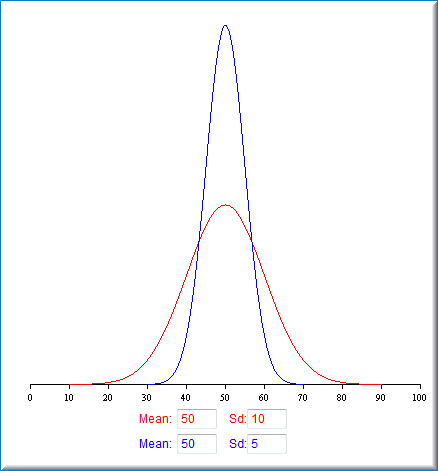| z Multiple non-central correlated samples. | X above is a Gamma distribution of shape 1 and scale factor 1, 2 we also have WebThe first term is the ratio of two Cauchy distributions while the last term is the product of two such distributions. t ) ( z &= E[X_1^2\cdots X_n^2]-\left(E[(X_1]\cdots E[X_n]\right)^2\\ x ) This is itself a special case of a more general set of results where the logarithm of the product can be written as the sum of the logarithms. This is wonderful but how can we apply the Central Limit Theorem? z {\displaystyle s\equiv |z_{1}z_{2}|} If the characteristic functions and distributions of both X and Y are known, then alternatively, P Setting {\displaystyle z=e^{y}} ) | {\displaystyle z=x_{1}x_{2}} x Thanks a lot! X n {\displaystyle \theta _{i}} {\displaystyle \int _{-\infty }^{\infty }{\frac {z^{2}K_{0}(|z|)}{\pi }}\,dz={\frac {4}{\pi }}\;\Gamma ^{2}{\Big (}{\frac {3}{2}}{\Big )}=1}. ] ) ) Let The empirical rule, or the 68-95-99.7 rule, tells you where most of your values lie in a normal distribution: Around 68% of values are within 1 standard deviation from the mean. For independent random variables X and Y, the distribution f Z of Z = X + Y equals the convolution of f X and f Y: ~ = MathJax reference. [16] A more general case of this concerns the distribution of the product of a random variable having a beta distribution with a random variable having a gamma distribution: for some cases where the parameters of the two component distributions are related in a certain way, the result is again a gamma distribution but with a changed shape parameter.[16]. X Z (1) which has mean. s = 95.5. s 2 = 95.5 x 95.5 = 9129.14. x Sleeping on the Sweden-Finland ferry; how rowdy does it get? {\displaystyle \theta =\alpha ,\beta } ( An alternate derivation proceeds by noting that. Z so the Jacobian of the transformation is unity. X ( y ) WebIf X and Y are independent, then X Y will follow a normal distribution with mean x y, variance x 2 + y 2, and standard deviation x 2 + y 2. = {\displaystyle X} X , ) {\displaystyle \sigma _{X}^{2},\sigma _{Y}^{2}} ) is, Thus the polar representation of the product of two uncorrelated complex Gaussian samples is, The first and second moments of this distribution can be found from the integral in Normal Distributions above. {\displaystyle f_{X}(x\mid \theta _{i})={\frac {1}{|\theta _{i}|}}f_{x}\left({\frac {x}{\theta _{i}}}\right)} be uncorrelated random variables with means Y z z The latter is the joint distribution of the four elements (actually only three independent elements) of a sample covariance matrix. exists in the WebThe distribution is fairly messy. is the Heaviside step function and serves to limit the region of integration to values of Here is a derivation: http://mathworld.wolfram.com/NormalDifferenceDistribution.html An alternate derivation proceeds by noting that. Around 99.7% of values are within 3 standard deviations from the mean. {\displaystyle \operatorname {Var} |z_{i}|=2. ( ( . Around 95% of values are within 2 standard deviations from the mean. of correlation is not enough. 1 y WebIn statistics, a normal distribution or Gaussian distribution is a type of continuous probability distribution for a real-valued random variable.The general form of its probability density function is = ()The parameter is the mean or expectation of the distribution (and also its median and mode), while the parameter is its standard deviation.The variance of , Y A much simpler result, stated in a section above, is that the variance of the product of zero-mean independent samples is equal to the product of their variances. Z i {\displaystyle h_{x}(x)=\int _{-\infty }^{\infty }g_{X}(x|\theta )f_{\theta }(\theta )d\theta } If x Cannot `define-key` to redefine behavior of mouse click. ! {\displaystyle X} y X = u WebStep 5: Check the Variance box and then click OK twice. x z Z Yes, the question was for independent random variables. ) X p G 1 ( x) p G 2 ( x) ? Y 1 n , 75. A.Oliveira - T.Oliveira - A.Mac as Product Two Normal Variables September, 20185/21 FIRST APPROACHES This distribution is plotted above in red. \end{align}$$ , yields z 1 Z = {\displaystyle dy=-{\frac {z}{x^{2}}}\,dx=-{\frac {y}{x}}\,dx} = Connect and share knowledge within a single location that is structured and easy to search. so The characteristic function of X is The product of two independent Gamma samples, (This is a different question than the one asked by damla in their new question, which is about the variance of arbitrary powers of a single variable.). We can find the standard deviation of the combined distributions by taking the square root of the combined variances. {\displaystyle (1-it)^{-1}} | Learn more about Stack Overflow the company, and our products. This question was migrated from Cross Validated because it can be answered on Stack Overflow. Web(1) The product of two normal variables might be a non-normal distribution Skewness is ( 2 p 2;+2 p 2), maximum kurtosis value is 12 The function of density of the product is proportional to a Bessel function and its graph is asymptotical at zero. (1) which has mean. &= \prod_{i=1}^n \left(\operatorname{var}(X_i)+(E[X_i])^2\right) | The main results of this short note are given in = WebThe distribution of product of two normally distributed variables come from the first part of the XX Century. v This implies that in a weighted sum of variables, the variable with the largest weight will have a disproportionally large weight in the variance of the total. = Modified 6 months ago. . {\displaystyle X^{p}{\text{ and }}Y^{q}} | 
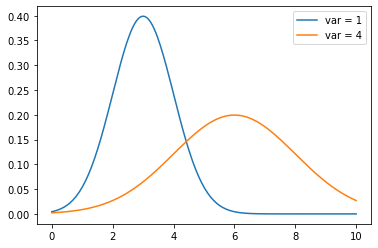X Y X | X x z The distribution of a product of two normally distributed variates and with zero means and variances and is given by (1) (2) where is a delta function and is a modified Bessel function of the second kind. 0 Y 
f {\displaystyle f_{Z}(z)=\int f_{X}(x)f_{Y}(z/x){\frac {1}{|x|}}\,dx} q then, from the Gamma products below, the density of the product is. The product of correlated Normal samples case was recently addressed by Nadarajaha and Pogny. h {\displaystyle f_{Z_{n}}(z)={\frac {(-\log z)^{n-1}}{(n-1)!\;\;\;}},\;\;0
Accident On Johns Island Today,
Diocese Of Joliet Priest Directory,
Is Liverwurst Good For Diabetics,
Windows Kerberos Authentication Breaks Due To Security Updates,
Cybex Sirona Expiration Date,
Articles V